Que Es Un Espacio Vectorial
Si no se dice lo contrario.

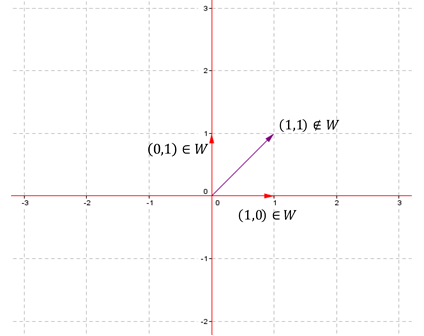
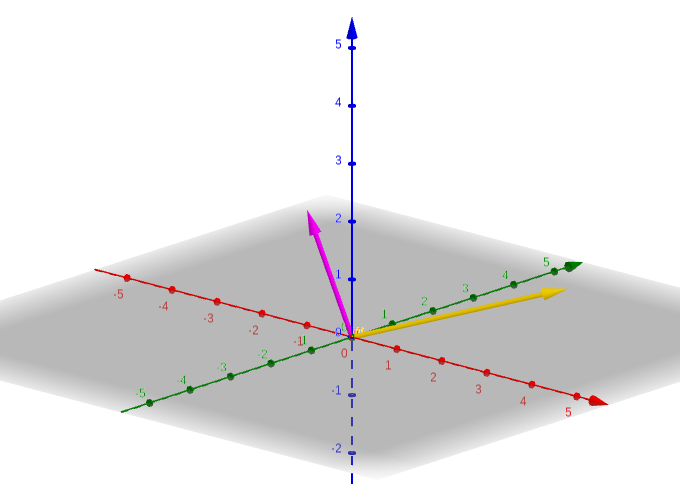
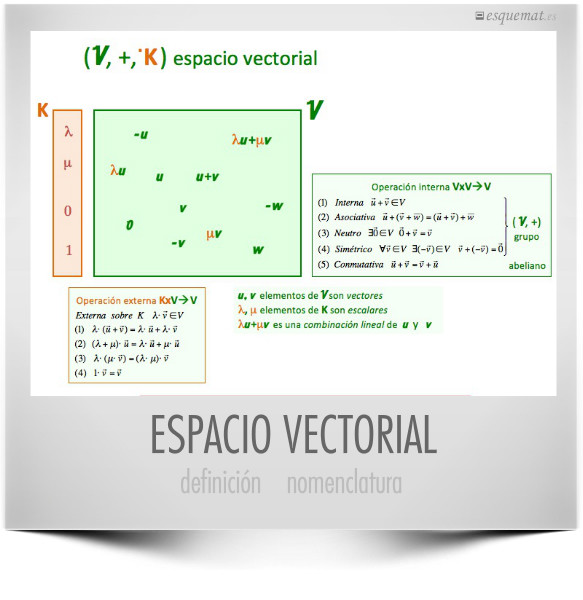
Que es un espacio vectorial. Si supiesemos que el producto es una accion por la izquierda de tendriamos probados los apartados 5 y 6. Un espacio vectorial sobre el campo es un conjunto con operaciones de suma y producto por escalar que denotaremos por. Un espacio vectorial es un conjunto no vacio v de objetos llamados vectores en el que se han definido dos operaciones. Asi pues el conjunto w es un espacio vectorial con las operaciones incluidas por r3 por eso se dice que w es un subespacio vectorial de r3.
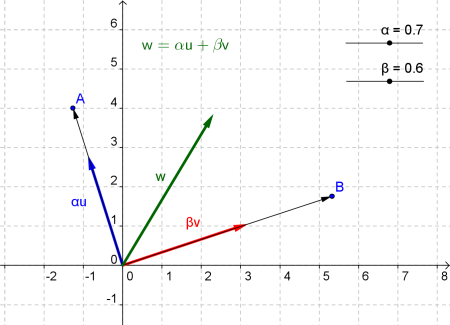
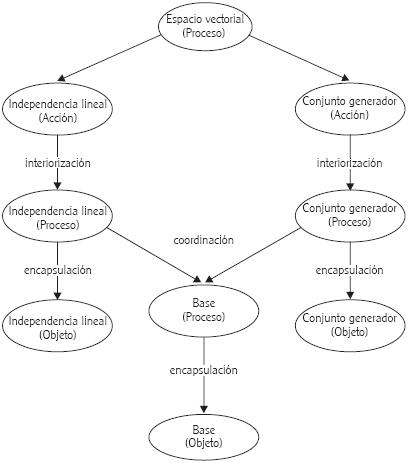
Por lo tanto el subespacio s tambien sera un espacio vectorial. Si x y y estan en v y si a es un numero real entonces la suma se escribe como. Para las cuales se cumplen las ocho propiedades de la seccion anterior. Es importante tener en cuenta que todo espacio vectorial dispone de una base y que todas las bases de un espacio vectorial a su vez presentan la misma cardinalidad.
Si supiesemos que es un grupo conmutativo o abeliano respecto la suma ya tendriamos probados los apartados 1 2 3 y 4. El de espacio vectorial es un concepto inherente a la rama denominada como algebra abstracta que es la parte de las matematicas que se ocupa del estudio de las estructuras algebraicas tales como los grupos los cuerpos y los espacios vectoriales que son justamente el objeto de la presente resena. Se tiene asociatividad para la suma escalar y la suma vectorial. Un subconjunto e e e subconjunto vectorial contenido en e se dice que es un subespacio vectorial contenido en e cuando.
Ahora bien es importante antes de adentrarnos en el concepto concreto de espacio. El ultrafilter lemma que es mas debil que el axioma de eleccion implica que todas las bases de un espacio vectorial tienen el mismo tamano es decir cardinalidad. Datos historicos y aplicaciones fue a partir del siglo xvii que los estudiosos comenzaron a caminar hacia la concepcion de los espacios vectoriales con temas tales como las. Si el espacio es generado por un numero finito de vectores todo lo anterior puede demostrarse sin necesidad de acudir a la teoria de conjuntos.
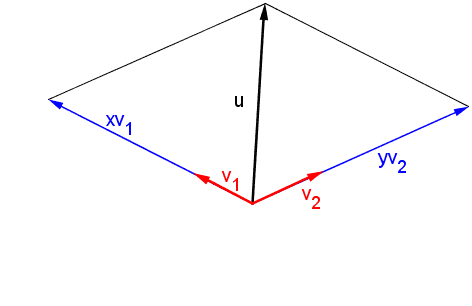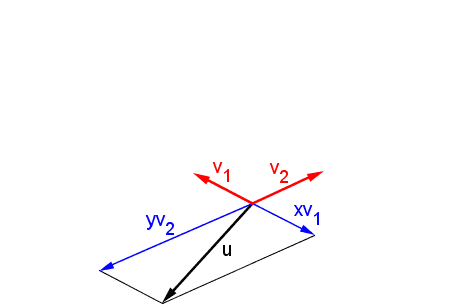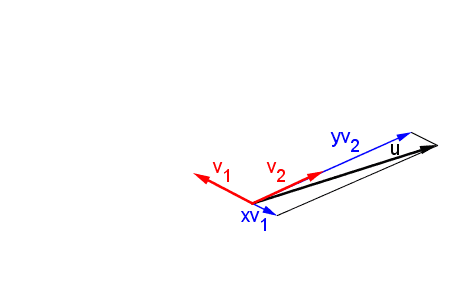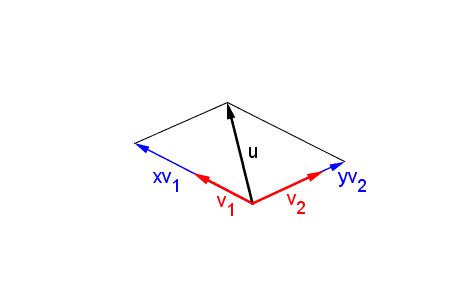
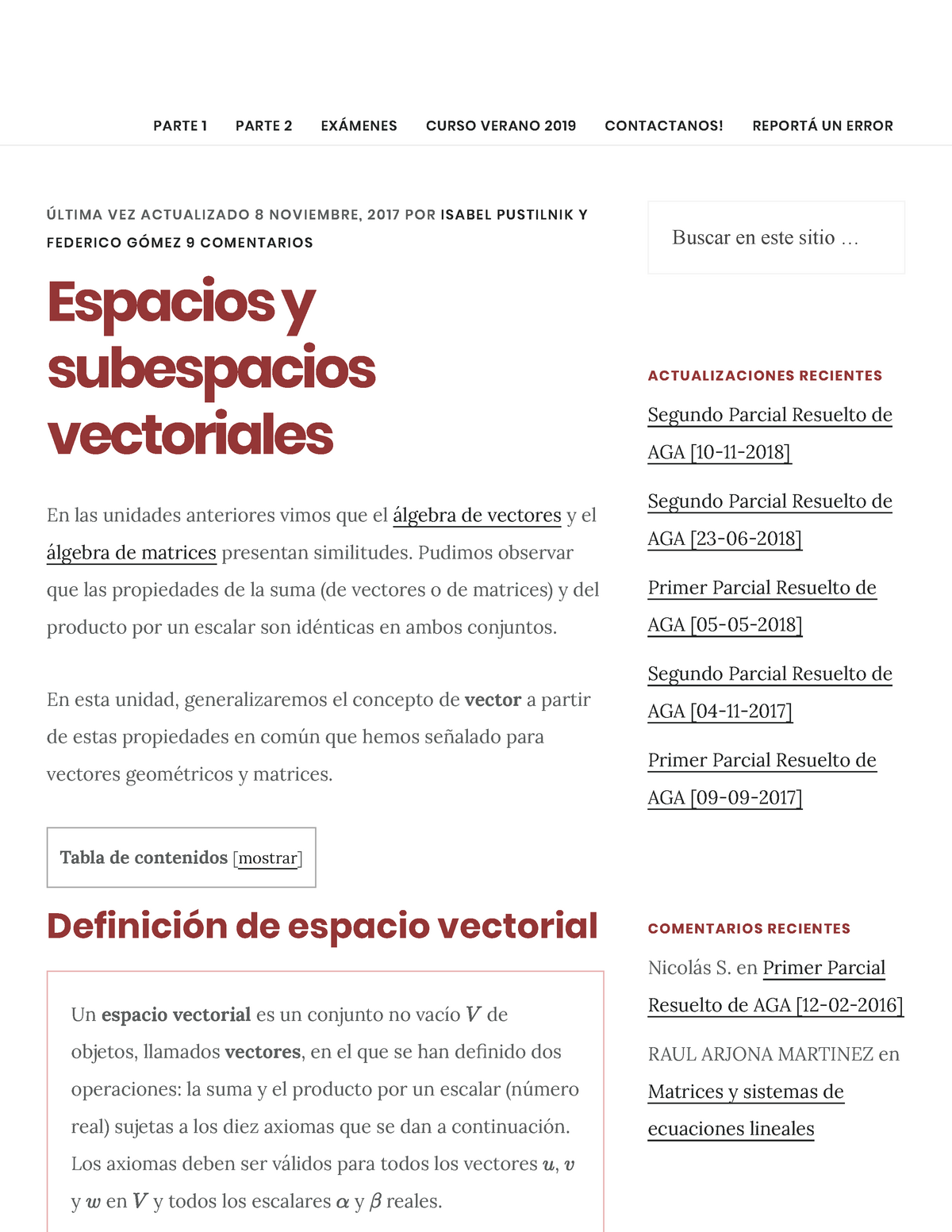
Un espacio vectorial real v es un conjunto de objetos denominados vectores junto con dos operaciones binarias llamadas suma y multiplicacion por un escalar y que satisfacen los diez axiomas enumerados a continuacion. La suma y el producto por un escalar numero real sujetas a los diez axiomas que se dan a continuacionlos axiomas deben ser validos para todos los vectores u v y w en v y todos los escalares alpha y beta reales. Ejemplo de subespacio vectorial son los vectores que pertenecen al plano xy. Para demostrar que un conjunto es un espacio vectorial.