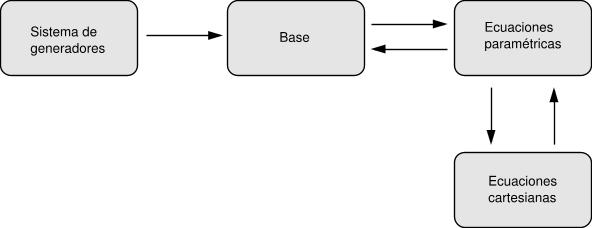
Que Es Un Subespacio Vectorial
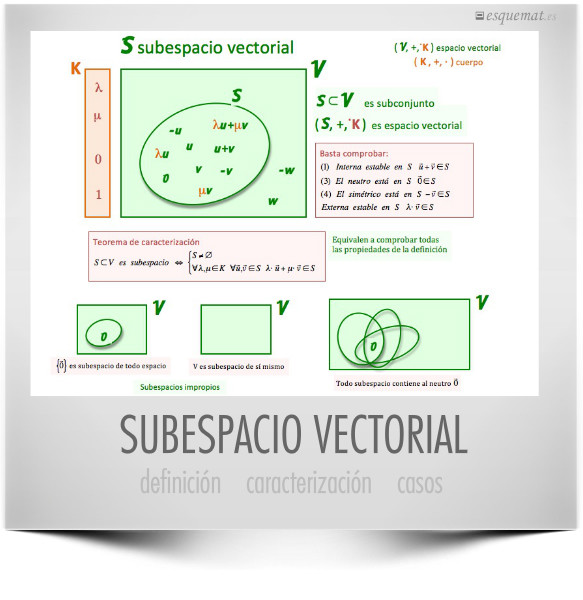
Definicion de sub espacio vectorial sea h un subconjunto no vacio de un espacio vectorial v y suponga que h es en si un espacio vectorial bajo las operaciones de suma y multiplicacion por un escalar definidas en v.
Que es un subespacio vectorial. Sea et2 un espacio euclideo si e es un espacio vectorial y t2 es un meretricia euclidea. Un espacio vectorial es un conjunto no vacio v de objetos llamados vectores en el que se han definido dos operaciones. Un subconjunto no vacio w de un espacio vectorial real v es un subespacio vectorial de v si y solo si w conjuntamente con las operaciones de suma y multiplicacion escalar definidas en v es en si mismo un espacio vectorial real. La nocion de subespacio topologico se presenta de manera natural y es el concepto analogo al de subgrupo en teoria de grupos o al de subespacio vectorial en algebra lineal.
Entonces se dice que h es un sub espacio de v. Una metrica t2 es euclidea si y solo si los menores diagonales de su matriz respecto de cualquier base son estrictamente positivos. Cerradura de la suma vectorial para cualesquiera y elementos de se cumple que esta en. Definicion de subespacios vectoriales reales definicion.
En otras palabras es un subespacio de si se cumplen las siguientes dos propiedades. Un subespacio vectorial de o simplemente un subespacio de es un subconjunto no vacio de cerrado bajo las operaciones de suma vectorial y multiplicacion escalar de. Subconjunto de v no vacio. Definicion de sub espacio vectorial sea h un subconjunto no vacio de un espacio vectorial v y suponga que h es en si un espacio vectorial bajo las operaciones de suma y multiplicacion por un.
Un subespacio vectorial s de un espacio vectorial v es un subconjunto de v en el que se definen las mismas operaciones que en v y cumple todos los axiomas de espacio vectorial. Ejemplo de subespacio vectorial son los vectores que pertenecen al plano xy. I si uv uentoncesuv u u es cerrado para. La suma y el producto por un escalar numero real sujetas a los diez axiomas que se dan a continuacion.
Por lo tanto el subespacio s tambien sera un espacio vectorial. Un conjunto de vectores es fundamental si la clausura topologica del subespacio vectorial que engendra es el espacio completo.